3.1.4. Практические соображения
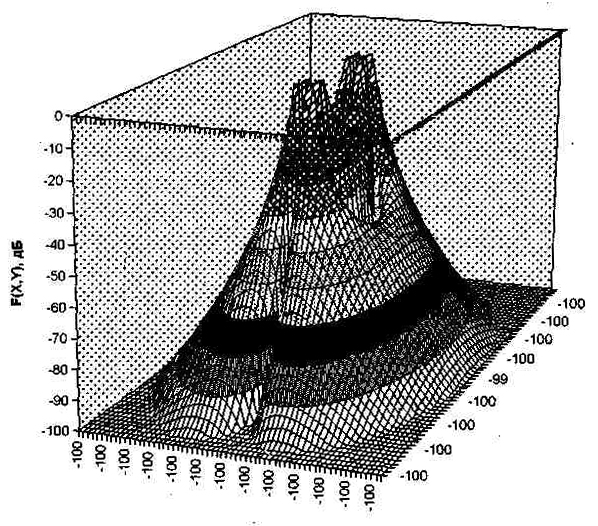
Чувствительность металлоискателя зависит, в первую очередь от его датчика. Для рассмотренных вариантов датчиков чувствительность определяется формулами (1.20) и (1.33). При оптимальной для каждого случая ориентации ориентации датчика на объект по углу крена y, она определяется одним и тем же коэффициентом K4 и функциями нормированных координат F(X,Y) и G(X,Y). Для сравнения, в квадрате ХО[-4,4], YО[-4,4], модули этих функций приведены в виде аксонометрического набора сечений в логарифмическом масштабе на рис.12 и рис.13.
Первое, что бросается в глаза - это ярко выраженные максимумы вблизи точек расположения катушек датчика (0,+1) и (0,-1). Максимумы функций F(X,Y) и G(X,Y) не представляют практического интереса и для удобства сравнения функций обрезаны по уровню 0(дБ). Из рисунков и из анализа функций F(X,Y) и G(X,Y) также видно, что в указанном квадрате модуль функции F практически везде немного превосходит модуль функции G, за исключением самых удаленных точек по углам квадрата и за исключением узкой области вблизи Х=0, где у функции F имеет место "овраг".
Асимптотическое поведение указанных функций вдали от начала координат можно проиллюстрировать при Y=0. Оказывается, что модуль функции F убывает с расстоянием пропорционально х^(-7), а модуль функции G - пропорционально х^(-6). К сожалению, преимущество функции G по чувствительности проявляется лишь на больших расстояниях, превышающих практический радиус действия

Рис. 12. График функции F(X,Y).
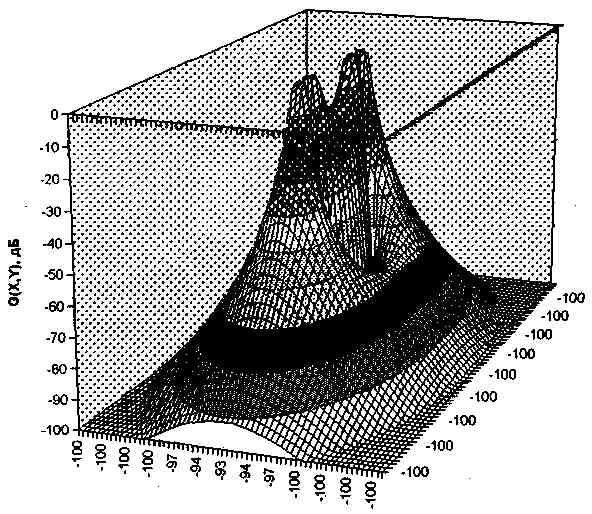
Рис.13. График функции G(X,Y).
металлоискателя. Одинаковые значения модулей F и G получаются при Х»4,25.
Очень важное практическое значение имеет "овраг" функции F. Во-первых, он свидетельствует о том, что датчик системы катушек с перпендикулярными осями имеет минимальную (теоретически нулевую) чувствительность к металлическим предметам, расположенным на его продольной оси. Естественно, к этим предметам относятся и многие элементы конструкции самого датчика. Следовательно, отраженный от них бесполезный сигнал будет намного меньше, чем у датчика системы катушек со скрещивающимися осями. Последнее очень важно, учитывая, что отраженный сигнал от металлических элементов самого датчика может на несколько порядков превосходить полезный сигнал (ввиду близости этих элементов к катушкам датчика). Дело не в том, что бесполезный сигнал от металлических элементов конструкции датчика трудно скомпенсировать. Основная сложность заключается в малейших изменениях этих сигналов, которые обычно вызываются тепловыми и особенно механическими деформациями указанных элементов. Эти малейшие изменения могут быть уже сопоставимы с полезным сигналом, что приведет к неверным показаниям или ложным срабатываниям прибора. Во-вторых, если с помощью металлоискателя системы катушек с перпендикулярными осями некоторый небольшой объект уже обнаружен, то направление его точного местонахождения может быть легко "запеленговано" по нулевому значению сигнала металлоискателя при точной ориентации его продольной оси на объект (при любых ориентациях по крену). Учитывая, что площадь "захвата" датчика при поиске может составлять несколько квадратньк метров, последнее качество системы катушек с перпендикулярными осями весьма полезно на практике (меньше бесполезных раскопок).
Следующая особенность графиков функцийF(X,Y) и G(X,Y) - наличие кольцеобразного "кратера" нулевой чувствительности, проходящего через центры катушек (окружность единичноо радиуса с центром в точке (0,0)). На практике эта особенность позволяет определять расстояние до небольших объектов. Если обнаружится, что на некотором конечном расстоянии отраженный сигнал зануляется (при оптимальной ориентации по крену) - значит, расстояние до объекта составляет половину базы прибора, то есть величину L/2.
Необходимо также отметить, что диаграммы направленности по углу крена y для датчиков металлоискателей с различным взаимным расположением катушек также различаются. На рис.14б приведена диаграмма направленности прибора с перпендикулярньми осями у катушек, а на рис.14а - со скрещивающимися. Очевидно, что вторая диаграмма более предпочтительна, так имеет меньшее количество зон нечувствительности по крену и меньшее количество лепестков.
Для того, чтобы оценить зависимость наведенного в приемной катушке напряжения от параметров металлоискателя и объекта, надо проанализировать выражение (1.19) для коэффициента К4. Наведенное в приемной катушке напряжение пропорционально (L/2)^6. На величину L/2 нормируются и аргументы функций F и G, убывание которых происходит с 6-й - 7-й степенью расстояния. Поэтому, в первом приближении, при прочих равных условиях, чувствительность металлоискателя не зависит от его базы.
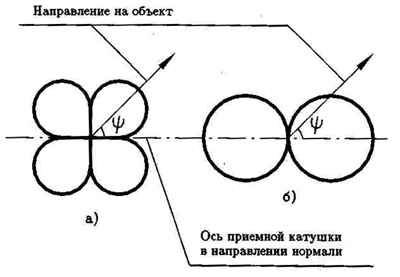
Рис.14. Диаграммы направленности по крену датчиков систем катушек:
- со скрещивающимися осями (а)
- с перпендикулярными осями (б).
Однако, в некоторых случаях конструкция датчика с большей базой может оказаться более предпочтительной, так как в этом случае меньшим будет неизбежное паразитное проникновение сигнала непосредственно из излучающей катушки в приемную.
Для того, чтобы проанализировать селективность металлоискателя, то есть его способность различать объекты, изготовленные из различных металлов или сплавов, необходимо обратиться к выражению (1.23). Металлоискатель может различать объекты по фазе отраженного сигнала. Для того, чтобы разрешающая способность прибора по типу металлов была максимальной, необходимо соответствующим образом выбрать частоту сигнала излучающей катушки, так, чтобы фаза отраженного от объектов сигнала составляла около 45°. Это - середина диапазона возможных изменений фазы первого слагаемого выражения (1.23), и там крутизна фазочастотной характеристики максимальна. Второе слагаемое выражения (1.23) считаем нулевым, так как при поиске в первую очередь нас интересует селективность по цветным металлам - неферромагнетикам. Естественно, оптимальный выбор частоты сигнала подразумевает знание типового размера предполагаемых объектов. Практически во всех зарубежных промышленных металлоискателях в качестве такого размера заложен размер монеты. Оптимальная частота составляет:

При типовом диаметре монеты 25(мм) ее объем составляет около 10^(-6) (м^3), что по формуле (1.25) соответствует эквивалентному радиусу около 0,6(см). Отсюда получаем оптимальное значение частоты около 1(кГц) при проводимости материала монеты 20(н0мЧм). В промышленных приборах частота обычно на порядок выше (по технологическим соображениям).