ЭКСПЕРИМЕНТ 22 Резонанс
Цели
После проведения данного эксперимента Вы сможете рассчитывать резонансную частоту резистивно-индуктивно-емкостной схемы и выполнять измерения в схеме для определения существования условия резонанса в схеме.
Необходимые принадлежности
* Осциллограф
* Цифровой мультиметр
* Макетная панель
* Генератор функций
* Элементы:
одна катушка индуктивности 10 мГн, один конденсатор 0, 22 мкФ, один конденсатор 0, 47 мкФ, один резистор 100 Ом.
ВВОДНАЯ ЧАСТЬ
Резонанс — это такое состояние резистивно-индуктивно-емкостной схемы, когда индуктивное сопротивление и емкостное сопротивление одинаковы. Поскольку эти реактивные сопротивления одинаковы, они полностью компенсируют друг друга. • При резонансе имеют место многие специальные эффекты. Например, в силу того, что реактивные
сопротивления полностью гасят друг друга, схема проявляет себя как полностью резистивная.
Вы сможете обнаружить резонансные схемы почти во всех типах электронного оборудования. Они широко используются для выполнения различных задач настройки и фильтрации в электронном оборудовании. В данном эксперименте Вы рассмотрите эффект резонанса как в параллельных, так и в последовательных схемах.
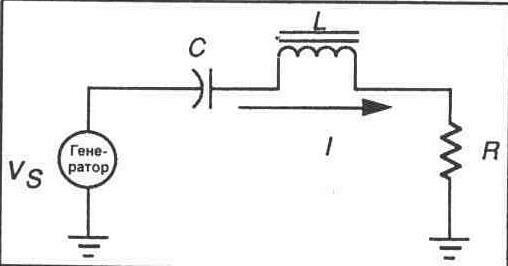
Последовательный резонансный контур
Последовательный резонансный контур представлен на рисунке 22-1. Вспомните, что при наличии резонанса в схеме индуктивное сопротивление и емкостное сопротивление полностью компенсируют друг друга, и сопротивление току оказывает одно лишь активное сопротивление схемы. В такой схеме полное сопротивление попросту равно значению R плюс сопротивление постоянному току катушки. Главной характеристикой последовательного резонансного контура является то, что его полное сопротивление минимально при резонансе. При настройке частоты на величину, превышающую или лежащую ниже резонансной частоты, полное сопротивление возрастает.
Поскольку при резонансе в последовательном резонансном контуре полное сопротивление минимально, ток в контуре возрастает до пиковой величины. Эта большая величина тока при ее умножении на индуктивное сопротивление и на емкостное сопротивление дает очень высокие падения напряжения на катушке индуктивности и на конденсаторе. В действительности падения напряжения на катушке индуктивности и на конденсаторе
в условиях резонанса часто значительно превышают напряжение питания. Эти необычайно высокие при резонансе напряжения называются скачками напряжения при резонансе или резонансными повышениями напряжения.

Рис. 22-1. Параллельный резонансный контур
Параллельный резонансный контур представлен на рисунке 22-2. Конденсатор и катушка индуктивности соединяются параллельно друг с другом, и вся комбинация иногда соединяется последовательно с резистором. Поскольку при резонансе индуктивное сопротивление и емкостное сопротивление полностью компенсируют друг друга, схема обнаруживает очень значительное активное сопротивление. В такой схеме полное сопротивление параллельного индуктивно-емкостного контура возрастает до многих тысяч Ом при резонансе. При частотах, превышающих или лежащих ниже резонансной частоты, полное сопротивление уменьшается.
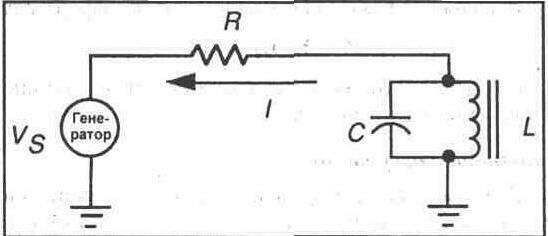
Рис. 22-2.
Если Вы измерите линейный ток в резисторе, соединенном последовательно с параллельным резонансным контуром, Вы обнаружите, что ток достигает минимума в условиях резонанса. Это происходит вследствие того, что при резонансе полное сопротивление максимально,и,следовательно, это приводит к формированию минимальной величины тока через контур. При изменении частоты в любую сторону от резонансной частоты полное сопротивление контура уменьшается, и линейный ток возрастает.
Полное сопротивление параллельного резонансного контура вычисляется на основании следующей формулы:
Z=L/CR
В этой формуле: R — сопротивление катушки индуктивности L. Например, если L = 2 мГн, С = 0,05 мкФ и R = 5 Ом, полное сопротивлений Z равно: '
Z = 2 х 10^-3 / (0,05 х 10 ^-6)(5)
Z = 8000 Ом
Вы можете также использовать такую формулу:
Z = Rw(Q^2 + 1)
где: Rw— это сопротивление обмотки катушки индуктивности и Q = Xl/Rw.
Краткое содержание
Как было указано ранее, в данном эксперименте Вы соберете последовательный резонансный контур и параллельный резонансный контур, а также познакомитесь с некоторыми из упомянутых эффектов. Вы практически рассчитаете резонансную частоту (fг ) при заданных значениях индуктивности и емкости. Это осуществляется при помощи следующей формулы:
fr = 1 / 2*3.14(LC)^0.5
ПРОЦЕДУРА
1. Обратитесь к рисунку 22-3. Рассчитайте резонансную частоту при заданных значениях, показанных на рисунке.
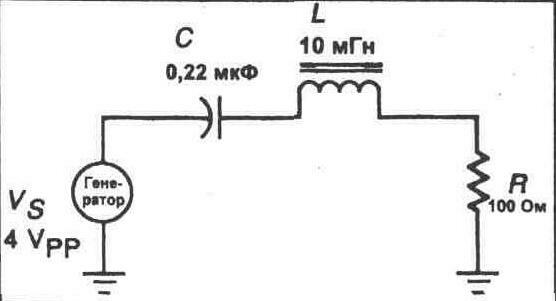
Рис. 22-3.
fr=______Гц
2. Прежде чем собирать схему, измерьте сопротивление катушки индуктивности. Это сопротивление оказывает влияние на полное сопротивление схемы.
Активное сопротивление катушки индуктивности = ____ Ом
ПРИМЕЧАНИЕ: Данные, полученные в шагах 3—11, должны заноситься в таблицу на рисунке 22-4, как указано ниже.
3. Вычислите полное сопротивление схемы при резонансе. Запишите Ваш результат.
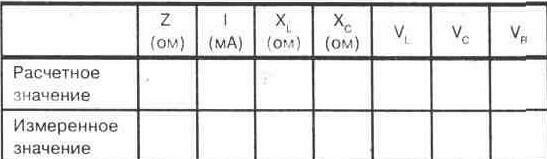
Рис. 22-4.
4. Далее вычислите полный ток схемы. Запишите его величину.
5. Зная частоту входного сигнала, определите значения индуктивного и емкостного сопротивления. Используя резонансную частоту, которую Вы рассчитали в шаге 1, вычислите определите значения индуктивного и емкостного сопротивления при резонансе. Запишите Ваши результаты.
6. Теперь вычислите падения напряжения на каждом из компонентов схемы на базе значений, полученных в шаге 5. Запишите Ваши результаты.
7. Соберите схему, показанную на рисунке 22-3. При помощи регулятора амплитуды на генераторе функций сформируйте значение размаха напряжения 4 В.
8. При помощи осциллографа осуществляйте мониторинг (текущий контроль) напряжения на резисторе 1000м. Во время мониторинга напряжения добейтесь максимального значения напряжения настройкой регулятора частоты на генераторе функций. Выполняйте Ваши настройки медленно и позволяйте показаниям мультиметра установиться, прежде чем переходить к каждой новой настройке. ПРИМЕЧАНИЕ: настройка на максимальное значение — процесс очень медленный и утомительный, потратьте однако Ваше время, чтобы получить наиболее точные результаты. Продолжайте настройку до тех пор, пока Вы не получите это максимальное напряжение. В результате Вы получили настройку генератора функций на резонансную частоту схемы. Объясните, почему данная процедура используется для нахождения fr .
9. Выполните повторный контроль, чтобы убедиться, что размах выходного напряжения генератора функций составляет 4 В. Если необходимо, снова отрегулируйте выходное напряжение на это значение и повторите при этом шаг 8.
10.После того, как схема настроена в режим резонанса, измерьте падения напряжения на каждом из компонентов. Запишите их значения.
11.Сделайте разрыв в схеме в том месте, где конденсатор 0,22 мкФ соединяется с катушкой, как
Вы это делали в предыдущем эксперименте. Это позволит Вам включить в схему мультиметр для измерения тока в схеме. Переключите Ваш мультиметр для измерения переменного тока. Установите предел измерения 2 мА. Измерьте ток в схеме и запишите Ваш результат.
12. Теперь сравните Ваши расчетные и измеренные значения. Они должны быть одинаковыми или, по крайней мере, очень близкими. Объясните возможные различия.
13. В процессе измерения тока в последовательном резонансном контуре варьируйте выход генератора функций при помощи регулятора частоты. Поворачивайте ручку медленно против часовой стрелки для уменьшения частоты и замечайте влияние на величину тока. Регулировка частоты должна выполняться настолько медленно, чтобы Вы могли наблюдать за изменениями показания мультиметра, так как требуется несколько секунд, чтобы показания установились после каждого нового изменения частоты.
Далее поворачивайте ручку медленно в направлении по часовой стрелке для увеличения частоты и снова замечайте влияние на величину тока. При изменении частоты выше или ниже резонансной частоты Вы обнаружите значительные вариации тока. Во время наблюдения за этими вариациями определяйте сразу, каким образом частота влияет на ток схемы.
14. Снова соедините катушку и конденсатор 0, 22 мкФ.
15. Присоедините измерительные выводы осциллографа к конденсатору и к катушке индуктивности одновременно. Варьируйте частоту при. помощи регулятора частоты на генераторе функций, чтобы получить минимальный уровень напряжения. Когда будет достигнуто минимально возможное напряжение, схема настроена в резонанс. Заметьте положение указателя, регулятора частоты на генераторе функций. Объясните, что Вы здесь получили;
16. Удалите конденсатор 0, 22 мкФ из макетной панели и на его место установите конденсатор 0, 47 мкФ. Вычислите резонансную частоту этой новой комбинации.
fr=____Гц
При увеличении емкости в схеме до 0,47 мкФ резонансная частота:
_________ увеличивается
_________ уменьшается
17.Снова присоедините измерительные выводы осциллографа к комбинации конденсатора и катушки индуктивности. Варьируйте частоту при помощи регулятора частоты на генераторе функций, чтобы получить минимальный уровень напряжения. Когда будет достигнуто минимальное напряжение, заметьте то направление, в котором Вы повернули регулятор генератора функций. Частота в данном случае выше или ниже, чем раньше? _________ выше
_________ ниже
Соответствует это результатам, которые предсказаны Вами в шаге 16?
18.Соберите параллельный резонансный контур, схема которого представлена на рисунке 22-5.
Заметьте, что два конденсатора включены последовательно и их комбинация соединена параллельно с катушкой индуктивности. Это соединение образует параллельный резонансный контур, в котором два последовательно включенных конденсатора имеют единственное эквивалентное значение емкости. Затем параллельный резонансный контур соединен последовательно с резистором 1 кОм, и вся полученная комбинация подключена к генератору функций.
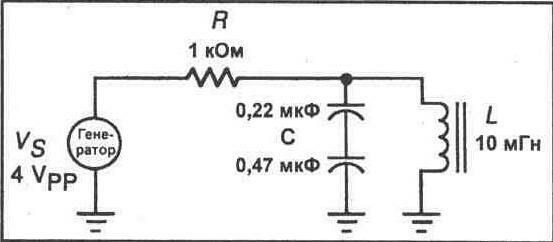
Рис. 22-5.
19. Вычислите резонансную частоту данной схемы. Индуктивность известна, но Вам требуется вычислить полную емкость схемы (Ст). Вспоминая, что Вы узнали ранее о последовательном включении конденсаторов, вычислите сначала полную емкость схемы. Запишите это значение. После этого вычислите резонансную частоту данной схемы и запишите Ваш результат в предусмотренное поле.
Ст = _______ мкФ
fr=_______Гц
20.Используя формулу, приведенную ранее для полного сопротивления параллельного резонансного контура, найдите это полное сопротивление. Используйте значение сопротивления катушки, которое Вы измерили в шаге 2.
Z =_______ Ом
21.Подайте на вход схемы синусоидальный сигнал с частотой 3 кГц. При помощи регулятора амплитуды на генераторе функций сформируйте значение размаха напряжения 4 В.
22.Осуществляйте мониторинг напряжения на резисторе 1 кОм при помощи осциллографа. Затем, варьируя частоту при помощи ручки регулятора частоты на генераторе функций, добейтесь минимального напряжения. Как и раньше, делайте это медленно и шагами. Слегка измените частоту и заметьте новое показание напряжения после того, как оно стабилизируется. Продолжайте настройку вперед и назад, пока Вы не добьетесь такой частоты, при которой напряжение минимально. Вы получили при этом резонансную частоту. Запишите в этот момент величину напряжения, которое Вы измерили на резисторе 1 кОм. Vr=_______В
23. Зная значение величины напряжения на резисторе с известным сопротивлением, Вы можете теперь вычислить величину полного тока схемы, используя закон Ома. Сделайте теперь вычисление и запишите значение величины тока.
I =_______ мА
24.Далее измерьте падение напряжения на параллельном резонансном контуре. Самый простой
способ сделать эти — просто прикоснуться испытательными выводами параллельно катушке индуктивности.
VLc=_______В
25.Зная значение величины напряжения на параллельном резонансном контуре и ток, который Вы нашли вычислением в предыдущем шаге, Вы можете теперь вычислить величину полного сопротивления индуктивно-емкостного контура. Сделайте теперь это вычисление и запишите Ваш результат.
Z=_______Ом
Как это значение соответствует значению, которое Вы нашли в шаге 20?
26.Сложите падение напряжения на резисторе 1 кОм и падение напряжения на параллельном резонансном контуре. Равна ли приблизительно эта сумма величине напряжения источника? Объясните Ваш ответ.
27.Соедините измерительные выводы вашего осциллографа с параллельным контуром, прикасаясь ими к двум выводам катушки индуктивности. Вращайте ручку регулятора частоты на генераторе функций в одну и в другую сторону от резонансной частоты и следите за изменением выходного напряжения. Ручку поворачивайте медленно из полностью выведенного в направлении против часовой стрелки положения в полностью выведенное в направлении по часовой стрелке положения, а затем назад, и так несколько раз, чтобы заметить эффект. Объясните вариации напряжения, которые Вы наблюдаете.
28.Выключите генератор функции, но схему пока не разбирайте.
ОБЗОРНЫЕ ВОПРОСЫ
1. Если конденсаторы 0,22 мкф и 0,47 мкФ подключены параллельно к катушке индуктивности 10 мГн, резонансная частота контура составляет:
а)1158 Гц,
б)1406 Гц,
в) 1917 Гц,
г) 2323 Гц.
2. Резонанс в последовательном контуре обнаруживается по:
а) максимальному току,
б) максимальному полному сопротивлению,
в) минимальному току,
г) нулевому току.
3. При резонансе параллельный резонансный контур ведет себя как:
а) резистор с малым сопротивлением,
б) резистор с большим сопротивлением,
в) катушка индуктивности,
г) конденсатор.
4. Каково полное сопротивление параллельного резонансного контура с L = 5 мГн, С == 0,001 мкФ и R =40м?
а) 84 кОм,
б) 125 кОм,
в) 840 кОм,
г) 1,25 МОм.
5. При резонансе в последовательной резистивно-индуктивно-емкостной схеме полное сопротивление равно:
а) XL или Xc
б) сопротивлению катушки индуктивности,
в) XL + Xc,
г) сопротивлению катушки индуктивности плюс сопротивление резистора.